When conducting data analysis of large groups of datasets, you’re likely to be overwhelmed by the amount of information it provides.
In such scenarios, it’s recommended to separate out these data points based on their similarities to make things easier to start with.
Have you ever heard of cluster analysis?
It’s an essential way of identifying discrete groups in data among many data professionals, yet many beginners remain in the dark about what cluster analysis is and how it works.
In this blog post, we’ll introduce you to the concept of cluster analysis, its advantages, common algorithms, how they can be evaluated, as well as some real-world applications.
We’ll cover the following:
- Cluster analysis: What it is and how it works
- What are the advantages of cluster analysis?
- Clustering algorithms: Which one to use?
- Evaluation metrics for cluster analysis
- Real-world applications of cluster analysis
- Key takeaways
Join us as we dive into the basics of cluster analysis to help you get started.
1. Cluster analysis: What it is and how it works
To help you better understand cluster analysis, let’s go over the definition of what it is first.
What is cluster analysis?
Cluster analysis is a statistical technique that organizes and classifies different objects, data points, or observations into groups or clusters based on similarities or patterns.
You can think of cluster analysis as finding natural groupings in data.
How does cluster analysis work?
Cluster analysis involves analyzing a set of data and grouping similar observations into distinct clusters, thereby identifying underlying patterns and relationships in the data.
Cluster analysis is widely used in data analytics across various fields, such as marketing, biology, sociology, and image and pattern recognition.
Cluster analysis varies by the type of clustering algorithm used.
2. What are the advantages of cluster analysis?
The concept of cluster analysis sounds great—but what are its actual advantages?
Here’s a list of them:
Identifying groups and relationships
Cluster analysis can help to identify groups and relationships in large datasets that may not be readily apparent.
This allows for a deeper understanding of the underlying structure of the data.
Likely the largest benefit of using cluster analysis is the ability to find similarities and differences in large datasets can help identify new trends and opportunities for further research.
Reducing data complexity
Cluster analysis can be used to reduce the complexity of large datasets, making it easier to analyze and interpret the data.
For example, by grouping similar objects together, the number of dimensions of data can be reduced. This might bring benefits of faster and more simplified analysis.
Clustering may also help rule out irrelevant data that do not have similarities. You’ll have a more streamlined analysis process as a result.
Improving visual representation
Cluster analysis often results in data visualizations of clusters, such as scatterplots or dendrograms.
These visualizations can be powerful tools for communicating complex information. Since cluster plots are simple for most to interpret and understand, this can be a good choice to include in presentations.
3. Clustering algorithms: Which one to use?
As mentioned, when starting a cluster analysis, you’re required to select from one of the appropriate clustering algorithms.
There are quite a few types of clustering algorithms out there, and each of them is used differently.
Here are the five most common types of clustering algorithms you’ll find:
1. Centroid-based clustering
Centroid-based clustering is a type of clustering method that partitions or splits a data set into similar groups based on the distance between their centroids.
Each cluster’s centroid, or center, is determined mathematically as either the mean or median of all the points in the cluster.
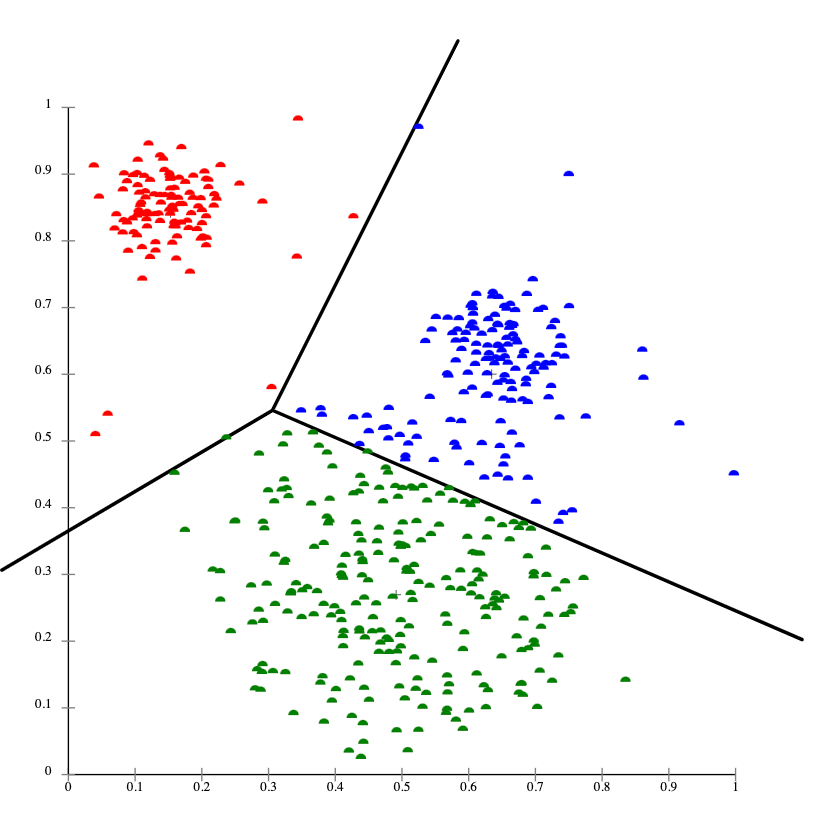
The k-means clustering algorithm is one commonly used centroid-based clustering technique. This method assumes that the center of each cluster represents each cluster.
It aims to find the optimal k clusters in a given data set by iteratively minimizing the total distance between each point and its assigned cluster centroid.
Other centroid-based clustering methods include fuzzy c-means.
2. Connectivity-based clustering
Connectivity-based clustering, also known as hierarchical clustering, groups data points together based on the proximity and connectivity of their attributes.
Simply put, this method determined clusters based on how close data points are to each other. The idea is that objects that are nearer are more closely related than those that are far from each other.
To implement connectivity-based clustering, you’ll need to determine which data points to use and measure their similarity or dissimilarity using a distance metric.
After that a connectivity measure (such as a graph or a network) is constructed to establish the relationships between the data points.
Finally, the clustering algorithm uses this connectivity information to group the data points into clusters that reflect their underlying similarities.
This is typically visualized in a dendrogram, which looks like a hierarchy tree (hence the name!).
3. Distribution-based clustering
Distribution-based clustering groups together data points based on their probability distribution.
Different from centroid-based clustering, it makes use of statistical patterns to identify clusters within the data.
Some common algorithms used in distribution-based clustering are:
- Gaussian mixture model (GMM)
- Expectation maximization (EM)
In the Gaussian mixture model (GMM), clusters are determined by finding data points that have a similar distribution.
However, distribution-based clustering is highly prone to overfitting, where clustering is too reliant on the data set and cannot accurately make predictions.
4. Density-based clustering
Density-based clustering is a powerful unsupervised machine learning technique that allows us to discover dense clusters of data points in a data set.
Unlike other clustering algorithms, such as K-means and hierarchical clustering, density-based clustering can discover clusters of any shape, size, or density.
Density-based clustering is especially useful when working with datasets with noise or outliers or when we don’t have prior knowledge about the number of clusters in the data.
Here are some of its key features:
- Can discover clusters of arbitrary shape and size
- Can handle noise and outliers
- Does not require specifying the number of clusters beforehand
- Can handle non-linear, non-parametric datasets
Here’s a list of some common density-based clustering algorithms:
- DBSCAN (Density-Based Spatial Clustering of Applications with Noise)
- OPTICS (Ordering Points To Identify the Clustering Structure)
- HDBSCAN (Hierarchical Density-Based Spatial Clustering and Application with Noise)
5. Grid-based clustering
Grid-based clustering partitions a high-dimensional data set into cells (disjoint sets of non-overlapping sub-regions).
Each cell is assigned a unique identifier called a cell ID, and all data points falling within a cell are considered part of the same cluster.
Grid-based clustering is an efficient algorithm for analyzing large multidimensional datasets as it reduces the time needed to search for nearest neighbors, which is a common step in many clustering methods.
4. Evaluation metrics for cluster analysis
There are several evaluation metrics for cluster analysis, and the selection of the appropriate metric depends on the type of clustering algorithm used and the understanding of the data.
Evaluation metrics can be generally split into two main categories:
- Extrinsic measures
- Intrinsic measures
Here are some common evaluation metrics for cluster analysis:
1. Extrinsic measures
Extrinsic measures use ground truth or external information to evaluate the clustering algorithm’s performance.
Ground truth data is the label data that confirms the class or cluster in which each data point belongs.
Extrinsic measures can be used when we know the true labels and want to evaluate how well the clustering algorithm is performing.
Common extrinsic measures include:
- F-measure/F-score: This metric determines the accuracy of the clustering algorithm by looking at precision and recall.
- Purity: This metric measures the fraction of data points that are correctly assigned to the same class or cluster they belong to.
- Rand index: This is a measure of the similarity between the true and predicted labels of the clustering algorithm, ranging from 0 to 1. A higher value indicates a better clustering performance.
2. Intrinsic measures
Intrinsic measures are evaluation metrics for cluster analysis that only use the information within the data set.
In other words, they measure the quality of the clustering algorithm based on the data points’ relationships within the data set. They can be used when we do not have prior knowledge or labels of the data.
Common intrinsic measures include:
- Silhouette score: This metric measures the similarity and dissimilarity of each data point with respect to its own cluster and all other clusters.
- Davies-Bouldin index: This metric calculates the ratio of the within-cluster distance to the between-cluster distance. The lower the index score, the better the clustering performance.
- Calinski–Harabasz index: Also known as the Variance Ratio Criterion, this measures the ratio of between-cluster variance and within-cluster variance. The higher the Calinski-Harabasz ratio, the more defined a cluster is.
These evaluation metrics can help us compare the performance of different clustering algorithms and models, optimize clustering parameters, and validate the accuracy and quality of the clustering results.
Using multiple evaluation metrics to ensure the clustering algorithms’ effectiveness and make robust decisions for cluster analysis is always recommended.
5. Real-world applications of cluster analysis
Cluster analysis is a powerful unsupervised learning technique that is widely used in several industries and fields for data analysis. Here are some real-world applications of cluster analysis:
1. Market segmentation
Companies leverage cluster analysis to segment their customer base into different groups.
Different customer attributes are analyzed, such as:
- age
- gender
- buying behavior
- location
Businesses can better understand their customer base and design targeted marketing strategies to meet their requirements.
2. Image segmentation in healthcare
Medical practitioners use clustering techniques to segment images of infected tissues into different groups based on certain biomarkers like size, shape, and color.
This technique enables clinicians to detect early signs of cancer or other diseases.
3. Recommendation engines
Large companies like Netflix, Spotify, and YouTube utilize clustering algorithms to analyze user data and recommend movies or products.
This technique examines user behavior data like clicks, duration on specific content, and the number of replays.
These data points can be clustered to find insights into user preferences and improve existing recommendations to users.
4. Risk analysis in insurance
Insurance companies utilize clustering analysis to segment various policies and customers’ risk levels.
By applying clustering techniques, an insurance company can better quantify the risk on their insurance policies and charge premiums based on potential risk.
5. Social media analysis
Social media apps can collect huge amounts of data from their users. The recent discussion around apps like TikTok or Meta’s new Twitter-like Threads are good reminders of this.
By clustering and examining their social interactions, users can be segmented based on age, demography, or purchasing behavior to lead to targeted ads, improving the overall engagement of ad placements.
6. Key takeaways
As you can see, cluster analysis is a powerful unsupervised learning technique.
To recap, here are some key takeaways:
- It brings many advantages when analyzing data, like streamlining analysis and representing data through visualizations.
- Clustering algorithms must be carefully selected according to their type for the best results.
- Extrinsic and intrinsic measures must be assessed to determine the effectiveness of your clustering.
- Cluster analysis can be applied to different industries.
What’s next? To get started with some practical work in data analytics, try out CareerFoundry’s, free 5-day data analytics course, or better still, talk to one of our program advisors to see how a career in data could be for you.
For more related reading on other areas within data analytics, check out the following:

